2025年单独招生考试

数学科目基本要求和考试大纲

一、考试目标

全面检测学生对数学课程内容的掌握程度，重点考查数学基础知识、基本技能、基本思想与基本活动经验，以及运用数学知识分析和解决实际问题的能力。通过考试引导学生形成良好的学习习惯、实践意识、创新意识及实事求是的科学态度，增强学生就业竞争力与创业能力。

二、考试内容及范围

1.集合(1) 理解集合、元素及其关系，空集的概念；(2) 掌握集合的表示方法；(3) 掌握集合间关系（子集、真子集、相等）；(4) 理解集合的运算（交、并、补）；

(5) 理解命题的概念；能分析"若p，则q"形式命题的逆命题、否命题与逆否命题，辨析四种命题的相互关系；理解必要条件、充分条件与充要条件的意义。

2.不等式

(1) 理解不等式的基本性质；

(2) 掌握区间的表示方法；

(3) 掌握一元二次不等式、一元一次不等式及分式不等式的解法；(4) 了解含绝对值不等式（|ax+b| <c或 >c）的解法。

3.函数

(1) 理解函数的概念；(2) 理解函数的三种表示方法；(3) 理解函数的单调性与奇偶性；(4) 会求函数的定义域及函数值；(5) 了解幂函数的概念及其简单性质。

4.指数函数与对数函数

(1) 理解有理指数幂，掌握实数指数幂的运算法则；

(2) 理解指数函数的概念、图像及其性质；

(3) 理解对数的概念（含常用对数、自然对数）及积、商、幂的对数运算；

(4) 理解对数函数的概念、图像及其性质。

5.三角函数

(1) 了解任意角的概念，理解弧度制的意义，熟练进行弧度与角度的换算；(2) 理解任意角的正弦函数、余弦函数及正切函数的概念；

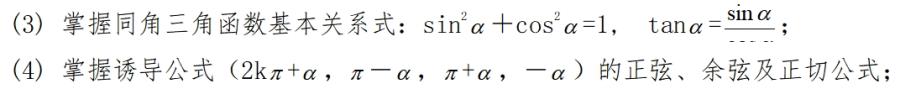
(5) 理解正弦函数、余弦函数的图像及其性质；

(6) 能根据三角函数值求指定范围内的特殊角。

6.数列

(1) 了解数列的概念；

(2) 理解等差数列的定义、通项公式及前n项和公式；

(3) 理解等比数列的定义、通项公式及前n项和公式。

7.平面向量

(1) 了解平面向量的概念；

(2) 理解平面向量的加法、减法及数乘运算；

(3) 理解平面向量的坐标表示；

(4) 理解平面向量的内积运算。

8.直线和圆的方程

(1) 掌握两点间距离公式及中点公式；

(2) 理解直线的倾斜角与斜率，掌握直线的点斜式、斜截式及一般式方程；

(3) 理解两条直线平行与垂直的条件，掌握求两条相交直线交点的方法；

(4) 了解点到直线的距离公式；

(5) 掌握圆的标准方程及一般方程；

(6) 理解直线与圆的位置关系。

9.实数、根式与分式

(1) 掌握实数的基本运算（含绝对值比较、倒数、四则运算及幂运算）；

(2) 理解二次根式成立的条件，掌握二次根式的运算；

(3) 掌握分式成立的条件及分式的四则运算。

10.多项式与方程

(1) 掌握单项式与多项式的基本运算及式子的化简变形；

(2) 能解一元一次方程、分式方程、一元二次方程，能根据实际问题建立方程或方程组并求解。

三、考试方案

（一）考试形式与时量

笔试、闭卷，考试时间为40分钟。

（二）试卷题型、题量及分值

试卷满分100分，题型、题量及分值如下：

（三）试卷难度

试题难度不超过中职毕业生水平，其中：较易题约占60%（基础知识和技能）；中等难度题约占30%（综合应用）；较难题约占10%（问题分析与迁移）。

（四）指定教材

①高等教育出版社，《数学》（主编：李广全、李尚志），2009年6月；

②语文出版社，《数学》（主编：张景斌），2009年7月；

③人民教育出版社，《数学》（主编：房艮孙），2009年6月；

④湖南科学技术出版社，《数学》（主编：杨向群），2009年7月。